Differencing Schemes
In the flux expressions (37.16), (38.6-38.11) and the pressure gradient terms (38.14) we calculate the values of the velocity components and pressure at the specified locations (“e”, “w”, “n”, “s”, “ne”, “se”, “nw”, “sw”) on the CV appear. These need to be expressed in terms of nodal values by means of suitable interpolation schemes. Several options are possible, the most natural one being linear interpolation, by which the values on the “e”- and “n”- CV faces are calculated as:
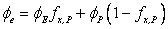
|
(40.1) |
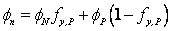 |
with 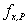 and and 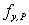 being linear interpolation factors: being linear interpolation factors:
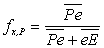
|
(40.2) |
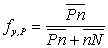 |
Such interpolation is referred to as Central Differencing Scheme (CDS). An alternative interpolation practice, which is also widely used, is the Upwind Differencing Scheme (UDS) Yielding:
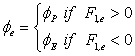
|
(40.3) |
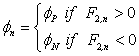 |
The CDS results in negative coefficients for the downstream neighbour nodes in Eqn (39.12) if convection dominates strongly over diffusion. The negative coefficients may cause unphysical oscillations in the solution. Sometimes the solution does not converge. The UDS, on the other hand, is unconditionally stable. However UDS introduces numerical errors known as “artificial” or “false” diffusion.
One can chose the option between using CDS, UDS or a combination of the two. The combination can be achieved via the so called “deferred correction” approach, i.e. the convection flux is taken to be:
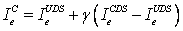 |
(40.4) |
If 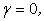 the convection fluxes are calculated from UDS Expressions, and if the convection fluxes are calculated from UDS Expressions, and if 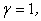 the CDS expressions are employed; for the CDS expressions are employed; for 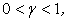 the two fluxes are blended. the two fluxes are blended. |