Equations (37.8) and (37.9) are to be integrated over a finite number of control volumes covering the solution domain. The time discretization will be discussed in a subsequent section.
Here, Gauss' divergence theorem is used, which transforms the volume integral of a vector divergence into a surface integral:
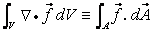 |
(37.10) |
V is the volume of an element, and A is the area of its surface, 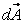 being the outward directed surface vector normal to this surface. The right hand side of Eq. (37.10) represents the net flux of the transported quantity through the control volume surface. It must be equal to the net source given by the right hand sides of Eqs. (37.8) and (37.9). In the case of the continuity equation, there is no source, i.e the net mass flux must be zero. For the momentum equations the right hand side being the outward directed surface vector normal to this surface. The right hand side of Eq. (37.10) represents the net flux of the transported quantity through the control volume surface. It must be equal to the net source given by the right hand sides of Eqs. (37.8) and (37.9). In the case of the continuity equation, there is no source, i.e the net mass flux must be zero. For the momentum equations the right hand side 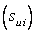 represents the external force (pressure and gravitational force expressed by Eq. (37.4). represents the external force (pressure and gravitational force expressed by Eq. (37.4).
The surface integrals are evaluated on each control volume face and summed up. For a two-dimensional case the third dimensional is unity, and the fluxes in this direction are zero.
Since the third dimension is unity, the cell face areas are equal to the length of the line segments connecting the two vertices.
The fluxes are by definition (Eq. (37.10)) taken positive when directed outwards. It should be noted that the outward flux through the “e”- cell face, Ie , is the inward flux through the “w”-cell face of the neighbouring control volume, i.e, 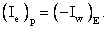 This can be advantageously used in the computer code, so that only two fluxes per control volume need to be calculated, namely This can be advantageously used in the computer code, so that only two fluxes per control volume need to be calculated, namely 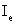 and and 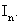 The general form of the discretized equation then becomes The general form of the discretized equation then becomes
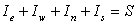 |
(37.11) |
Where the I's represent the cell face fluxes,
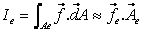 |
(37.12) |
The surface vector on the cell faces are defined as ( for “e”- and “n”- cell faces):
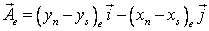 |
(37.13) |
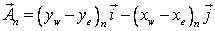 |
|