Discretization of the fluid domain for Continuity and Momentum equations
In this section, the discretization procedure for the continuity and momentum equations for fluid flow is described. The procedure for the scalar equation of energy transport will be illustrated subsequently.
Thus, in general, the present method provides the possibility for computation of the following flow field variables,
- Velocity component in the x direction: U1= U
- Velocity component in the y direction: U2= V
- Velocity component in the z direction: U3= W
- Pressure P
- Temperature T
For two-dimensional flow, the flow field in the plane remains invariant in all the planes parallel to it. For axisymmetric cases, U, V and W respectively represent the axial, radial and circumferential components of the velocity field  . .
For turbulent flow, averaged forms of the continuity and momentum equations together with the transport equations for turbulent kinetic energy and the dissipation rate can be solved. The flow field variables represent time averaged mean values. Turbulent flows, however, are not considered in this lecture.
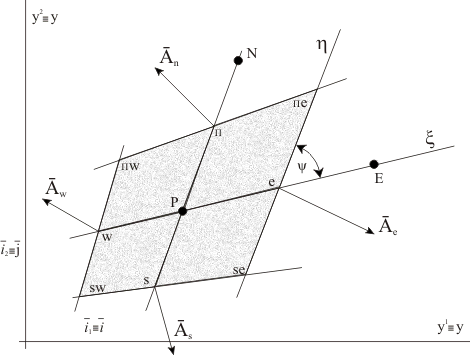
Figure 37.1: Coordinate System and base Vectors
Fig. 37.1 shows the Cartesian coordinate system 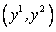 with base vector with base vector  and and 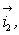 and a typical control volume together with the identification of the important points. and a typical control volume together with the identification of the important points.
|