The discretized representations of the continuity and momentum equations are as the following.
In the case of continuity equation, the vector 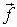 in Eqs. (37.10) and (37.12) stands for in Eqs. (37.10) and (37.12) stands for 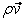 . The positive, outward directed fluxes through the east and north cell faces become: . The positive, outward directed fluxes through the east and north cell faces become:
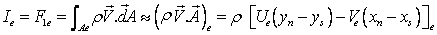 |
(37.14) |
F1 and F2 denote the average mass fluxes in the positive coordinate x1 , x2 , respectively. The continuity equation can be written as:
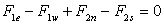 |
(37.15) |
Ue ,Ye ,Un and 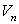 in Eqs. (37.14) represent the average values of the Cartesian velocity components at the appropriate cell faces. The procedure of calculating these values from the nodal values are described later. in Eqs. (37.14) represent the average values of the Cartesian velocity components at the appropriate cell faces. The procedure of calculating these values from the nodal values are described later.
The left hand side of the momentum equations (Eq.(37.2) has two parts: convection and diffusion. These will be treated separately. For the convection fluxes 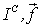 in Eqs. (37.10) and (37.12) is substituted by in Eqs. (37.10) and (37.12) is substituted by 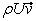 for U - equation yielding: for U - equation yielding:
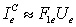
|
(37.16) |
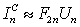 |
|
In the case of the diffusion fluxes, ID , the vector 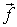 stands in the U - equation for stands in the U - equation for 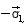 see Eqs. (37.3) and (37.4). Thus according to Eq. (37.12) we get: see Eqs. (37.3) and (37.4). Thus according to Eq. (37.12) we get:
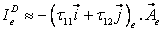
|
(37.17) |
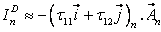 |
|
Congratulations, you have finished Lecture 37. To view the next lecture select it from the left hand side menu of the page or click the next button. |