Thomas algorithm
In Crank Nicolson solution procedure, we get a system of algebraic equations which assumes the form of a tridiagonal matrix problem. Here we shall discuss a very well known solution procedure known as Thomas algorithm (1949) which utilizes efficiently the advantage of the tridiagonal form. A tridiagonal system is:
The Thomas Algorithm is a modified Gaussian matrix-solver applied to a tridingonal system.
The idea is to transform the coefficient matrix into a upper triangular form. The intermediate steps that solve for x1, x2, ...xN .
Change di and ci arrays as
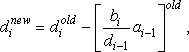 i = 2,3,....N i = 2,3,....N |
|
and
Similarly
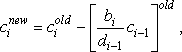 i = 2,3,....N i = 2,3,....N |
|
and
At this stage the matrix is in upper triangular form. The solution is then obtained by back substitution as
and
|