Some Non-Trivial Problems with Discretized Equation
The discussion in this section is based upon some ideas indicated by Hirt (1968) which are applied to model Burger's equation as
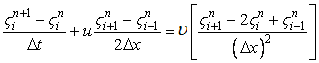 |
(13.4) |
From this, the modified equation becomes
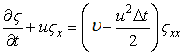 |
(13.5) |
We define
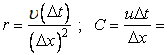 Courant number Courant number |
|
It is interesting to note that the values 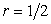 and C=1 (which are extreme conditions of Von Neumann stability analysis) unfortunately eliminates viscous diffusion completely in Eq. (13.5) and produce a solution from Eq. (13.4) directly as and C=1 (which are extreme conditions of Von Neumann stability analysis) unfortunately eliminates viscous diffusion completely in Eq. (13.5) and produce a solution from Eq. (13.4) directly as 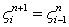 which is unacceptable. From Eq. (13.5) it is clear that in order to obtain a solution for convection diffusion equation, we should have which is unacceptable. From Eq. (13.5) it is clear that in order to obtain a solution for convection diffusion equation, we should have
For meaningful physical result in the case of inviscid flow we require
Combining these two criteria, for a meaningful solution
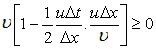 |
(13.6) |
Here we define the mesh Reynolds-number or cell-peclet number as
So, we get
or
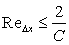 |
(13.7) |
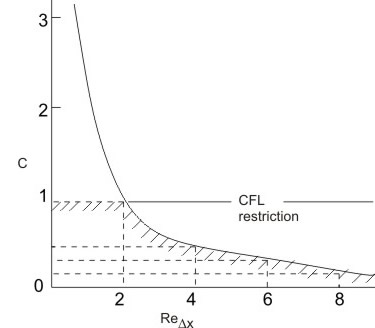
Figure 13.1: Limiting Line ( 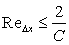 ) )
The plot of C vs 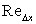 is shown in Fig. 13.1 to describe the significance of Eq. (13.7). is shown in Fig. 13.1 to describe the significance of Eq. (13.7).
From the CFL condition, we know that the stability requirement is  Under such a restriction, below Under such a restriction, below 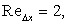 the calculation is always stable. The interesting information is that it is possible to cross the cell Reynolds number of 2 if C is made less than unity. the calculation is always stable. The interesting information is that it is possible to cross the cell Reynolds number of 2 if C is made less than unity.
|