Problems
(1) Consider the nonlinear equation
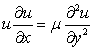 |
(13.8) |
where μ is a constant and u the x component of velocity. The normal direction is y.
(a) Is this equation in conservative from? If not, suggest a conservative from of the equation.
(b) Consider a domain in to x ( x = 0 to x = L) and y (y = 0 to y = H) and assume that all the value of the dependent variable are known at x = 0 (along y = 0 to y = H at every y interval). Develop an implicit expression for determining u at all the points along (y=0 to y=H) at the next (x+Δx)
(2) Establish the truncation error of the following finite-difference approximation to 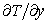 at the point at the point 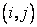 for a uniform mesh for a uniform mesh
What is the order of the truncation error ?
If you want to apply a second-order-accurate boundary condition for 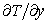 at the boundary (refer to Fig. 13.2), can you make use of the above mentioned expression? If yes, what should be the expression for at the boundary (refer to Fig. 13.2), can you make use of the above mentioned expression? If yes, what should be the expression for 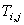 at the boundary? at the boundary?
(3) The lax-Wendroff finite difference scheme (Lax and Wendroff, 1960) can be derived from a Taylor series expansion in the following manner:
Using the wave equations
the Taylor series expression may be written as
Prove that the CFL condition is the stability requirement for the above discretization scheme.
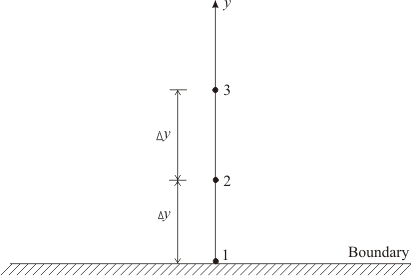
Figure 13.2: Grid points at a boundary
(4) A three-level explicit discretization of
can be written as
Expand each term as a Taylor series to determine the truncation error of the complete equation for arbitary values of d. Suggest the general technique where for a functional relationship between d and 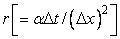 the scheme will be fourth-order accurate in the scheme will be fourth-order accurate in 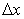 . .
(5) Consider the equation
where T is the dependent variable which is convected and diffused. The independent variable, x and y, are in space while t is the time (evolution) coordinate. The coefficient u,v and α can be treated as constant. Employing forward difference for the first-order derivative and central-second difference for the second derivatives, obtain the finite-difference equation. What is the physical significance of the difference between the above equation and the equation actually being solved? Suggest any method to overcome this difference.
(6) Write down the expression for the Finite Difference Quotient for the convective term of the Burger's Equation given by
|
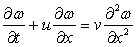 |
(13.9) |
Use upwind differencing on a week conservative from of the equation. The upwind differencing is known to retain the transportive property. Show that the formulation preserves the conservative property of the continuum as well [you are allowed to exclude the diffusive term from the analysis].
|