Second Upwind Differencing or Hybrid Scheme (Contd...)
Let us discretize the second term of the convection part of unsteady x- direction momentum equation. We have chosen this in order to cite a meaningful example of second upwind differencing. Using Eq. (12.5), we can write
Here we introduce a factor 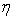 which can express Eq. (12.6) as a weighted average of central and upwind differencing. which can express Eq. (12.6) as a weighted average of central and upwind differencing.
Invoking this weighted average concept in Eq. (12.6), we obtain
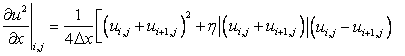 |
|
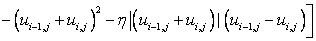 |
(12.7) |
where 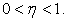 For For 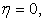 Eq (12.7) becomes centred in space and for Eq (12.7) becomes centred in space and for 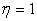 it becomes full upwind. it becomes full upwind.
Therefore 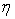 brings about the upwind bias in the difference quotient. If brings about the upwind bias in the difference quotient. If 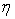 is small, Eq. (12.7) tends towards centred in space. This upwind method was first introduced by Gentry, Martin and Daly (1966). is small, Eq. (12.7) tends towards centred in space. This upwind method was first introduced by Gentry, Martin and Daly (1966).
Some more stimulating discussions on the need of upwind - and its minimization has been discussed by Roache (1972) who has also pointed out the second upwind- formulation possesses both the conservative and transportive property provided the upwind factor (formally called donorcell factor) is not too large.
In principle, the weighted average differencing scheme can as well be called as hybrid scheme (see Rairhby and Torrence, 1974) and the accuracy of the scheme can always be increased by a suitable adjustment of 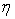 value. value.
|