Second Upwind Differencing or Hybrid Scheme
According to the second upwind differencing, if u is the velocity in x direction and 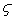 is any property which can be convected or diffused, then is any property which can be convected or diffused, then
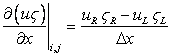 |
(12.1) |
One point to be carefully observed from Eq. (12.1) is that the second upwind should be written in conservative form.
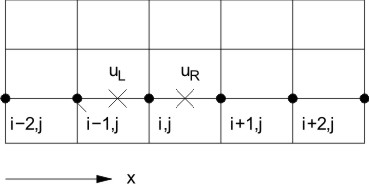
Figure 12.1: Definition of uR and uL
Definition of 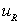
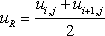 |
(12.2a) |
Definition of 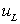
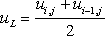 |
(12.2b) |
Now,
and
Finally, for 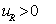 and and 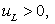 we get we get
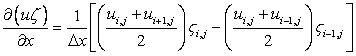 |
(12.5) |
|