Some More Suggestions for Improvements
Several researches have tried to resolve the difficulty associated with the discretization of the first-order terms which need some amount of artificial viscosity for stability. Substantial progress has been made on the development of higher-order scheme which are suitable over a large range of velocities. However, none of these prescriptions are universal. Depending on the nature of the flow and geometry one can always go for the best suited algorithm. Now we shall discuss one such can algorithm which has been proposed by Khosla and Rubin (1974).
Consider the Burger's equation. (9.11) once again. The derivatives in this equation are disceretizated in the following way.
For 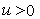
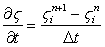 (Forward time) (Forward time) |
|
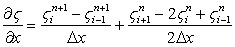 |
|
This is modified central difference in space, which for a converged solution 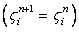 reduce to space centred scheme. reduce to space centred scheme.
Now, consider the diffusion term
This is central difference in space. Substituting the above quotients in Eq. (9.11), one finds
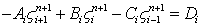 |
(12.8) |
where
and
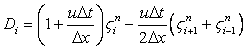 |
(12.9) |
For 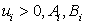 and and 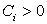 and and 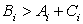 . .
The system of equation produced from Eq. (12.8) is always diagonally dominant and capable of providing a stable solution. As the solution progresses ( i.e. 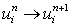 ),the convective term approaches second-order accuracy. ),the convective term approaches second-order accuracy.
This method of implementing higher-order upwind is known as the “deferred correction procedure”.
Congratulations, you have finished Lecture 12. To view the next lecture select it from the left hand side menu of the page or click the next button. |