Upwind Differencing and Artificial Viscosity
Consider the model Burger's equation. (9.11) and focus the attention on the inertia terms
As seen, the simple upwind scheme gives
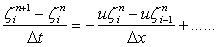 for u > 0 for u > 0 |
|
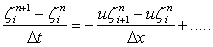 for u < 0 for u < 0 |
|
From Taylor series expansion, we can write
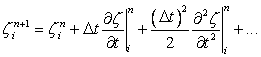 |
(11.8) |
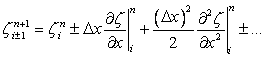 |
(11.9) |
Substituting Eqns. (11.8) and (11.9) into (11.3) gives (dropping the subscript i and superscript n)
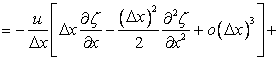 [Diffusive terms] [Diffusive terms] |
|
or
which may be rewritten as
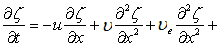 higher order terms higher order terms |
(11.10) |
where
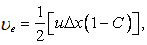 C (Courant number) C (Courant number) 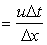 |
|
In deriving Eq. (11.10), 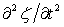 was taken as was taken as 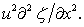 . .
However, the nonphysical coefficient 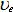 leads to diffusion like term which is dependent on the discretization procedure. This leads to diffusion like term which is dependent on the discretization procedure. This 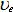 is known as the numerical or artificial viscosity. is known as the numerical or artificial viscosity.
Let us look at the expression somewhat more critically..
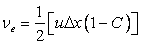 , for u > 0 , for u > 0 |
(11.11) |
On one hand we have considered that u > 0 and on the other CFL condition demands that C < 1 (so that the algorithm can work).
As a consequence, 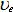 is always a positive non-zero quantity ( so that the algorithm can work). is always a positive non-zero quantity ( so that the algorithm can work).
If, instead of analyzing the transient equation, we put 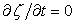 in Eq. (11.3) and expand it in Taylor series, we obtain in Eq. (11.3) and expand it in Taylor series, we obtain
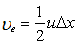 |
(11.12) |
|