Transportive Property
A finite-difference formulation of a flow equation possesses the transportive property if the effect of a perturbation is convected (advected) only in the diprection of the velocity.
Consider the model Burger's equation in conservation form
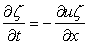 |
(11.5) |
Let us examine a method which is central in space. Using FTCS we get
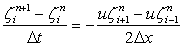 |
(11.6) |
Consider a perturbation 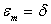 in in 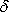 . .
A perturbation will spread in all directions due to diffusion. We are taking an inviscid model equation and we want the perturbation to be carried along only in the direction of the velocity. So, for 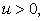 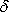 (perturbation at mth space location), all other (perturbation at mth space location), all other 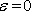 . .
Therefore, at a point (m+1) downstream of the perturbation
which is acceptable. However, at the point of perturbation ( i=m)
which is not very reasonable. But at the upstream station ( i = m-1 ) we observe
which indicated that the transportive property is violated.
On the contrary, let us see what happens when an upwind scheme is used.
We know that for u>0
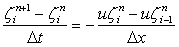 |
(11.7) |
Then for 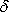 at the downstream location (m+1) at the downstream location (m+1)
which follows the rational for the transport property.
At point m of the disturbance
which means that the perturbation is being transported out of the affected region.
Finally, at ( m−1) station, we observe that
This signifies that no perturbation effect is carried upstream. In other words, the upwind method maintains unidirectional flow of information.
In conclusion, it can be said that while space centred difference are more accurate than upwind differences, as indicated by the Taylor series expansion, the whole system is not more accurate if the criteria for accuracy includes the tranportive property as well.
|