The Upwind Scheme
Once again, we shall start with the inviscid Burger's equation. (9.12) Regarding discretization, we can think about the following formulations
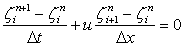 |
(11.1) |
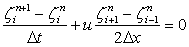 |
(11.2) |
If Von Neumann's stability analysis is applied to these schemes, we find that both are unconditionally unstable.
A well known remedy for the difficulties encountered in such formulations is the upwind scheme which is described by Gentry, Martin and Daly (1966) and Runchal and Wolfshtein (1969).
Eq. (11.1) can be made stable by substituting the forward space difference by a backward space difference scheme, provided that the carrier velocity u is positive. If u is negative, a forward difference scheme must be used to assure stability. For full Burger's equation. (9.11), the formulation of the diffusion term remains unchanged and only the convective term (in conservative form) is calculated in the following way (Figure 11.1):
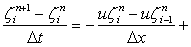 viscous term, for viscous term, for 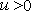 |
(11.3) |
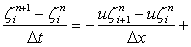 viscous term, for viscous term, for 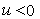 |
(11.4) |
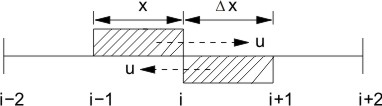
Figure 11.1: The Upwind Scheme
It is also well known that upwind method of discretization is very much necessary in convection (advection) dominated flows in order to obtain numerically stable results.
As such, upwind bias retains transportative property of flow equation. Let us have a closer look at the transportative property and related upwind bias.
|