Let us now consider a two-dimensional convective-diffusive equation with viscous diffusion in both directions (Eq. (8.13) but with 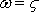 . .
For  upwind differencing gives upwind differencing gives
The Taylor series procedure as was done for Eq. (11.10) will produce
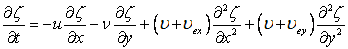 |
(11.14) |
where
As such for 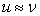 and and  CFL condition is CFL condition is 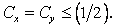
This indicate that for a stable calculation, artificial viscosity will necessarily be present. However, for a steady-state analysis, we get
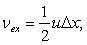 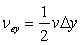 |
(11.15) |
We have observed that some amount of upwind effect is indeed necessary to maintain transportive property of flow equations while the computations based on upwind differencing often suffer from false diffusion (inaccuracy!). One of the plausible improvements is the usage of higher-order upwind method of differencing.
In the next lecture we'll discuss this aspect of improving accuracy.
Congratulations, you have finished Lecture 11. To view the next lecture select it from the left hand side menu of the page or click the next button. |