Boundary & Initial Conditions
The spatial boundary conditions in flow and heat transfer problems are of three general types. They may be stated as
 and  denote three separate zones on the bounding surface in Fig. 1.1.
The boundary conditions in Eqns. (1.7) to (1.9) are usually referred to as Dirchlet, Neumann and mixed boundary conditions, respectively. The boundary conditions are linear in the dependant variable  .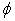
In Eqns. (1.7) to (1.9),  is a vector denoting position on the boundary,  is the directional derivative normal to the boundary, and  and  are arbitrary functions. The normal derivative may be expressed as
Here  is the unit vector normal to the boundary,  is the nabla operator, [.] denotes the dot product,  are the direction-cosine components of and  are the unit vectors aligned with the coordinates.
| 
