Finite Differences
- Analytical solutions of partial differential equations provide us with closed-form expressions which depict the variation of the dependent variable in the domain.
- The numerical solutions, based on finite differences, provide us with the values at discrete points in the domain which are known as grid points.
Consider Fig. 1.2, which shows a domain of calculation in the 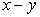 plane. plane.
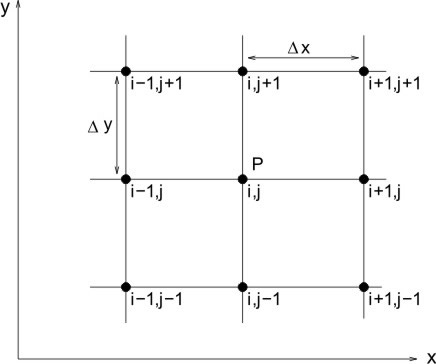
Figure 1.2; discrete Grid Points
Let us assume that the spacing of the grid points in the 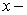 direction is uniform, and given by direction is uniform, and given by 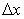 . Likewise, the spacing of the points in the . Likewise, the spacing of the points in the 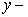 direction is also uniform, and given by direction is also uniform, and given by 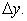
It is not necessary that 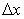 or or 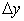 be uniform. We could imagine unequal spacing in both directions, where different values of be uniform. We could imagine unequal spacing in both directions, where different values of 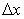 between each successive pairs of grid points are used. The same could be presumed for between each successive pairs of grid points are used. The same could be presumed for 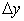 as well. as well.
However, often, problems are solved on a grid which involves uniform spacing in each direction, because this simplifies the programming, and often results in higher accuracy.
In some class of problems, the numerical calculations are performed on a transformed computational plane which has uniform spacing in the transformed-independent-variables but non-uniform spacing in the physical plane.
These typical aspects will be discussed later.
At present let us consider uniform spacing in each coordinate direction. According to our consideration, 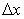 and and 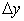 are constants, but it is not mandatory that are constants, but it is not mandatory that 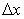 be equal to be equal to 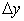 |