Classification of Partial Differential Equations
The parabolic equation in conduction heat transfer is of the form
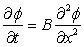 |
(1.4) |
The one-dimensional unsteady conduction problem is governed by this equation when 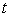 and and 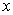 are identified as the time and space variables respectively, are identified as the time and space variables respectively, 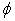 denotes the temperature and B is the thermal diffusivity. The boundary conditions at the two ends and `an initial condition are needed to solve such equations. denotes the temperature and B is the thermal diffusivity. The boundary conditions at the two ends and `an initial condition are needed to solve such equations.
The unsteady conduction problem in two-dimension is governed by an equation of the form
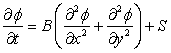 |
(1.5) |
Here 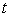 denotes the time variable, and a souce term S is included. By comparing the highest derivatives in any two of the independent variables, with the help of the conditions given earlier, it can be concluded that Eq. (1.5) is parabolic in time and elliptic in space. An initial condition and two conditions for the extreme ends in each special coordinates is required to solve this equation. denotes the time variable, and a souce term S is included. By comparing the highest derivatives in any two of the independent variables, with the help of the conditions given earlier, it can be concluded that Eq. (1.5) is parabolic in time and elliptic in space. An initial condition and two conditions for the extreme ends in each special coordinates is required to solve this equation.
Fluid flow problems generally have nonlinear terms due to the inertia or acceleration component in the momentum equation. These terms are called advection terms. The energy equation has nearly similar terms, usually called the convection terms, which involve the motion of the flow field. For unsteady two-dimensional problems, the appropriate equation can be represented as
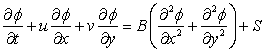 |
(1.6) |
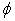 denotes velocity, temperature or some other transported property, denotes velocity, temperature or some other transported property,
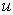 and and 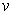 are velocity components, are velocity components,
B is the diffusivity for momentum or heat, and
S is a source term.
The pressure gradients in the momentum or the volumetric heating in the energy equation can be appropriately substituted in S. Eq. (1.6) is parabolic in time and elliptic in space.
For very high-speed flows, the terms on the left side dominate, the second-order terms on the right hand side become trivial, and the equation becomes hyperbolic in time and space.
|