Classification of Partial Differential Equations

In this slide we'll discuss Mathematical aspects of the equations that describe fluid flow and heat transfer problems.

Laplace equations:     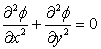(1.2)   Poisson equations:     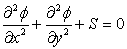(1.3)

Laplace equations and Poisson equations are elliptic equations and generally associated with the steady-state problems.

The velocity potential in steady, inviscid, incompressible, and irrotational flows satisfies the Laplace equation.

The temperature distribution for steady-state, constant-property, two-dimensional condition satisfies the Laplace equation if no volumetric heat source is present in the domain of interest and the Poisson equation if a volumetric heat source is present.