22.1 Shock-Shock Interaction

Interaction of two shocks is of great interest for various reasons. The major reason is the prediction of the flow field after interaction. This flowfield is greately dependant on the the family of the shock (right running or left running) and strength of the shocks in turn freestream properties. Aerodynamics of the body higly dependant on the shock-shock (S/S) interation. Edney* has defined six types of shock shock interactions based on family and strength of the interacting shocks and post shock flowfield. Herewith, basics of the shock shock interation are mentioned.

* B. Edney, Anomalous heat transfer and pressure distributions on blunt bodies at hypersonic speeds in the presence of an impinging shock, Aeronautical Research Institute of Sweden, Report 115, Stockholm (1968).

22.2 Ineraction of shocks of differet family

Lets consider the situation given in Fig.22.1 to understand the S/S interaction for shocks from two different families.

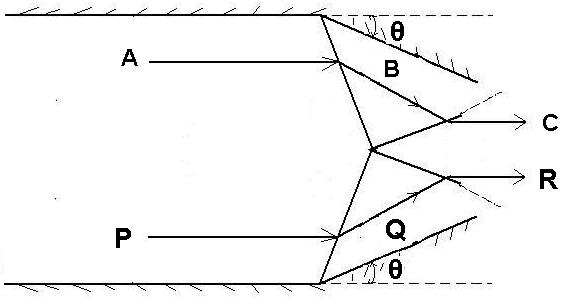
Fig, 22.1. Typical example of S/S interaction of shocks of different families and same strength.

Here the righ running shock originated from the top wedge interacts with the left running shock originated from the bottom wedge, hence this is the S/S interaction for shocks of different families. For simplicity we have considered flow delfection angles to be same (θ) for both the wedges.The top wedge, in this situation, is responsible for right running shock wave while bottom wedge is responsible for left running shock wave. Now consider ths streamline ABC passing through the right running shock and PQR passing through the left running shock. The right running shock wave induces negative deflection to the streamline ABC at B, while left running shock wave induces positive deflection to the streamline PQR at Q. The corresponding increase in pressure associated with the flow turning are shown in Fig. 22.2 using the P- θ diagram. Here we can clearly see that points A & P are identical in this plot, since both the point are in the region upstream of shocks. Since streamline ABC gets negative deflection and streamline PQR gets positive deflection of same magnetude, points B and Q represent same pressure but different delfections of same magnetude. Suppose, both the shocks are weak enough to keep the flow supersonic in the region given by points B and Q of the streamlines. The flow properties will be indentical donwstream of the first shocks (at B and Q), except the y-direction velocity. After interaction we can see that two different shocks originate from the interaction point. The main reason for this shock formation is to avoid the collision and intersection of streamlines ABC and PQR. Therefore, streamline ABC passes through a left running shock and streamline PQR passes through the right running shock wave. Hence the further pressure rise is evident in Fig. 22.2 in the presence of post interaction shocks.

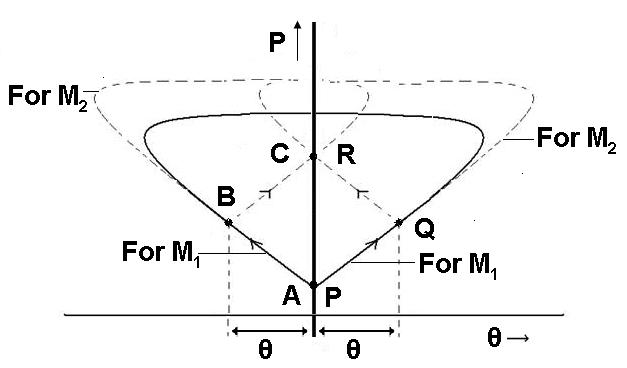
Fig, 22.2. Pressure deflection diagram for S/S interaction of shocks of different families and same strength.

Moreover, these shocks cancel out the deflection so as to make the both the streamlines parallel to each other without avoiding their crossing. For flow downstream of first shock, we have to draw the pressure-deflection diagram from points B & Q respectively corresponding to their Mach numbers (which are identical in the present situation). Again it can be seen that, points C and R represent same pressure and deflection.