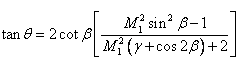19.2 θ-β-M relation

It has been already observed that the Mach number normal to the shock is repsonsible for all the property variations for given shock angle. However this shock angle can be easily calculated from the upstream or freestream Mach number for given wedge or deflecion angle. Consider the same control volume shown in Fig.18.3. Reation between velocties and angles before and after the shocks are,

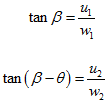Before the shock After the shock

But we know that,

w₁ = w₂
Hence,

But
ρ₁u₁ = ρ₂u₂ hence,

Therefore,

From density ratio Eq (5.4), we have

From the expression of upstream Mach number,

 

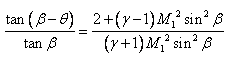
19.7

This is the expression between upstream Mach number, shock angle and wedge angle. In most general case, we need to know the shock angle for given Mach number and wedge angle. Following figure provides the information about the same (Fig. 19.1). In this figure, each curve corresponds to various possible shock angles for a given Mach number and flow deflection angle.

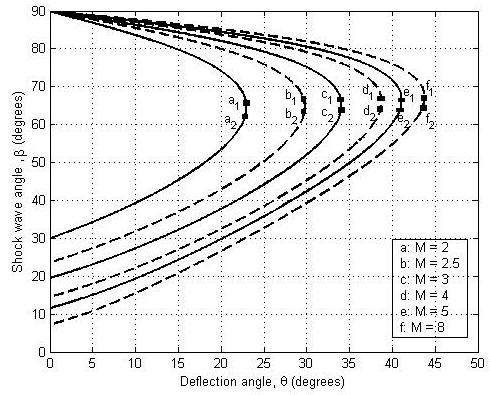
Fig. 19.1 θ-β-M relation

Following points should be noted from this figure.

1. For a given Mach number and wedge angle, there are two possible shock angles.The lower shcok angle corresponds to a weak shock solution and higher shock angle corresponds to strong shock solution. Weak shock solution is the most familiar solution or situation we encounter in the nature. Higher shock angle values, obtained out of two possible solutions for the given Mach number and delfection angle, is referred as the strong shock stolution. The strong shock solution may exist for a given Mach number and deflection angle if the pressure on the wedge can be increased independantly. However this situation is most uncommon. Points having subscript 1 in Fig. 19.1 are the reference points for the known Mach number above which shock is said to be strong shock and below which shock is said to be weak shock. Points having subscript 2 in Fig. 19.1 are the reference points for the known Mach number above which shock flow behind the shock is subsonic and below which flow behind the shock is supersonic.
2. If we consider the weak shock solution, then for a given Mach number, increase in deflection angle increases the shock angle. Thus Increased shock angle decreases the Mach number behind the shock. Hence shock strength increases for a given Mach number with increase in deflection angle. For a particular deflection angle, we get, maximum shock angle for a given Mach numer above which there is no attached shock solution. Hence there exists no solution or deflection angle for that Mach number for which shock is attached. This situation is discribed in Fig. 19.2.

   
   
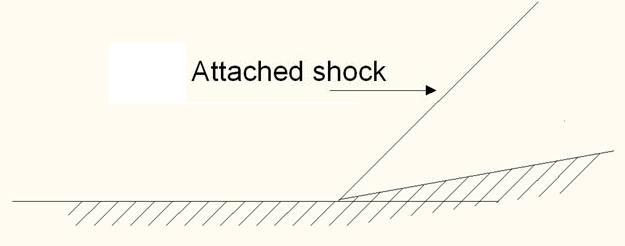
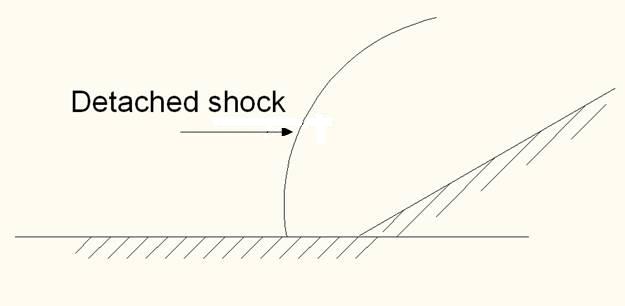
   Fig. 19.2. Attached and detached shock solutions.

3. If we consider the weak shock solution, then, for a given deflection angle, increase in Mach number decreases the shock angle and shock becomes weaker.
4. All the curves for various Mach numbers can be seen to meet at 90 degree shock angle for zero degree delfection angle. This situation corresponds to normal shock. However, the other solution for
   zero degree deflection angle corresponds to Mach angle, μ=sin-1(1/M). Therefore intersection of the curve with shock angle for weak solution for all the Mach number is different.