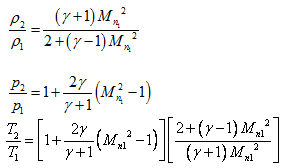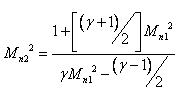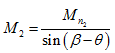19.1 Oblique Shock
We have already derived the mass and momentum conservation equations for the oblique shock conditions. Consider the integral form of energy equation for inviscid compressible flow.
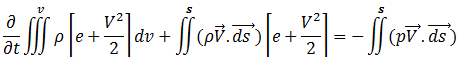
For steady flow,this equation changes to,
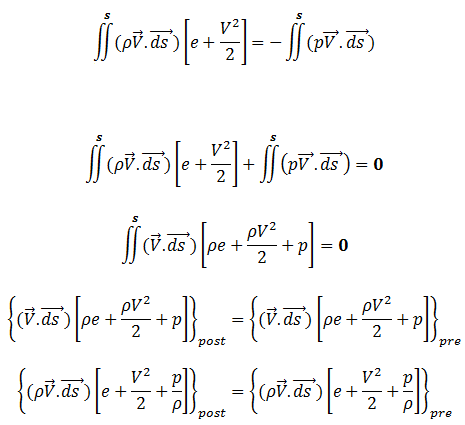
But,
![]()
Hence the energy equtation can be written as,
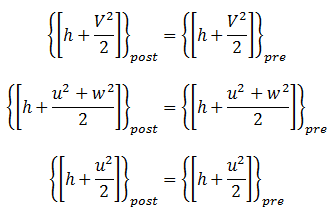
![]()
Hence,
|
19.1 |
Energy equation is also similar as that of energy equation for normal shock. Here 'u' is the velocity normal to the shock. From mass, momentum and energy equations, it is clear that, only velocity normal to the shock, is responsibile for change in all the properties. Hence we can still use all the equation of static and total property ratios derived for normal shock relations by changing the freestream Mach number to Mach number normal to the shock.
If freestream or upstream Mach number and the shock angle are known, then we can calculate the Mach number normal to the shock as,
![]()
Prandtl's relation for the oblique shock is,
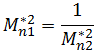
This relation suggests that, for oblique shock, normal Mach number before or upstream to the shock is supersonic and hence normal Mach number after or downstream to the shock is subsonic.
The static propety ratios for oblique shock are,
|
19.2
19.3 19.4 |
Total property ratios can be re-written in the same way. We can as well calculate the Mach number behind the shock as,
|
|
|
19.6 |