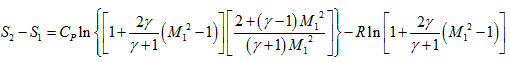Expression for static enthalpy ratio across the shock will be same as the static temperature ratio given by (7.4).

Following things are clear from the property ratios,

• All the ratios are dependant on freestream Mach number and specific heat ratio (γ), where Mach number is flow property and specific heat ratio is fluid property.
• Static pressure ratio, 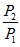, increases with increase in γ for same freestream Mach number. Hence, 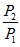will be more for air than carbon-dioxide for the same Mach number since γ for carbon-dioxide is 1.28 while for air is 1.4. The variation in γ can occur for the same gas due to dissociation, ionization or vibrational excitation, combustion, mixing of two gasses of different specific heat ratios etc.
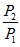• increases with increase in Mach number for same γ (for same gas).
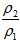• ratio increases with increase in Mach number for same γ (for same gas).
• Density ratio, 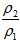, increases with decrease in γ, so for carbon-dioxide although it has lower 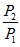for a given Mach number and γ, it will have higher .
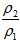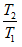• has the same behavior as 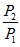where it increases with increase in M and γ.
• Each 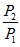and 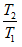→ ∞ as M → ∞. However 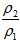attains a constant value, 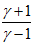, as M→ ∞. For air ((γ = 1.4) that constant value is 6.

• Mach number behind shock decreases as freestream Mach number increases. However, as M1→ ∞, M2 attains a constant value 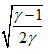which is 0.378 for air (γ = 1.4)
• Mach number behind the normal shock (M2 ) increases as γ increases for a given freestream Mach number.
  
  
• We know that entropy change in any process can be estimated as,

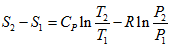
We can express the static temperature and pressure ratios in terms of freestream Mach number, Hence,

7.5

From this expression it is clear that the entropy change would be positive if and only if M1 > 1. That means shock is present only for supersonic flows and not for subsonic flows according to second law of thermodynamics.

• We know that 1D energy conservation equation is 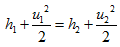If we image that the gas is isentropically brought to zero velocity on either side of the shock then the enthalpies would be stagnation enthalpies.
  ∴ h₀₁ = h₀₂
  ∴ C_pT₀₁ = C_pT₀₂
  ∴T₀₁ = T₀₂
  This expression re-asserts that flowfield is adiabatic since total temperature of the gas remains constant across the shock. Hence compression through shock is adiabatic irreversible.

• We can use already derived isentropic relation of total denisty to static density, eq. (6.3), to obtain the total density ratio across the shock.

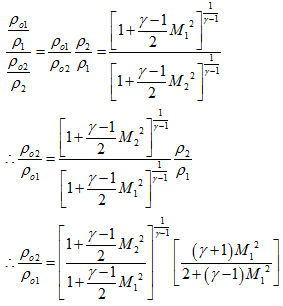
• 7.6

  
  Similarly we can find out the total pressure ratio across the shock using the isentropc relation given by eq. (6.2).
  

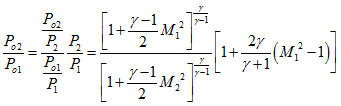
  7.7

  
  Total pressure and total density ratios are of same magnitude for the ideal gas conditions, since total temperature remains constant across the shock
  
  This can be proved using ideal gas equation.
  
  
  

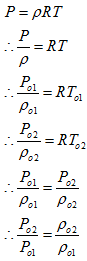
  We have derived all the static and total property ratios as function of M1 & γ, however, we can always express these relations as function of M2 & γ, since M2 is also function of M1.
  

  We can calculate the entropy change across the shock given by eq. (7.5) using the presently derived ratios,
  

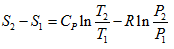
  7.8

  If we imagine that the gas element is isentropically brought to zero on either sides of shock then
  
  
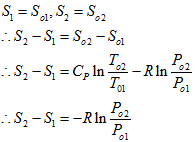
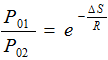
  This proves that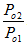 is less than 1 since Δs is positive for shocked flow. This expression suggests that the total pressure decreases across the normal shock.