7.1 Deivation for Mach number based on starred quantities:

The Prandtl's expression gives the relation between the starred acustic speed based Mach numbers ahead and behind the shock. Using this expression, we can prove that M₁^*2 > 1 which leads to M₂^*2 < 1. Let’s derive the expression initially for M*

Recall the equation (6.4) and (6.5) and express in general as,



Dividing by square of velocity,

7.1

Which clearly proves that, for M > 1, M* > 1 for M = 1, M* = 1 and M < 1, M* < 1

Therefore, from Prandtl’s relation (6.6)

where M₁ > 1 ⇒ M₁^*2 > 1 & M₂ < 1 ⇒ M₂^*2 < 1

This clearly proves that, any supersonic flow while pass through normal shock attains subsonic speed behind it.

From known freestream Mach number or the Mach number ahead of the shock we can calculate the Mach number behind the shock using Prandtl’s relation.


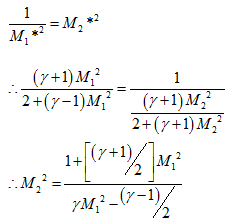
We can derive the expression for the properties behind the shock wave using 1D conservation equations and know properties ahead the shock.

7.2

This equation gives the density ratio which is function of freestream Mach number and the specific heat ratio. We can find out the velocity ratio from this density ratio as,

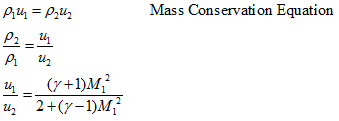
Let's derive the expression for static presure ratio. For simplicity of derivation, initially representation of dynamic pressure is necessary and can be expressed as follows

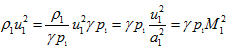From definition of Mach number
We know the 1D momentum conservation equation as
p₁ + ρ₁u₁² = p₂ + ρ₂u₂²
Replacing the dynamic pressure from either side and rearranging we get

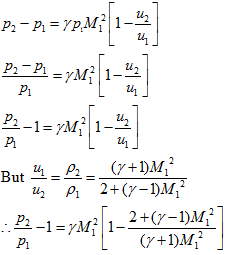
7.3

This equation gives the static pressure ratio which is again function of freestream Mach number and the specific heat ratio. Temperature ratio can be obtained from the pressure and density ratio as,

7.4