1.4.2. Transport phenomenon:
Diffusion of mass, mometum and heat always take place from the region of higher concentration to the region of lower concentration.
Concentration gradient of mass leads to mass transfer. Fick's law gives the quantification of mass transport through the linear relation between massflux and gradient of concentration. The proportionality constant (mass diffusion coefficient) depends on gases involved in the diffusion and their thermodynamic state. According to this law, diffusion of nitrogen in oxygen is different from diffusion of nitrogen in methane. Diffusion of nitrogen in oxygen also depends on pressure and temperature conditions. Sainted stick is the example of concentraion based mass diffusion.
Temperature variation leads to heat transfer. Fourier's law gives the relation between heatflux and gradient for temperature. The proportionality constant is the material property (thermal conductivity) and depends mainly on temperature of the material. Heat transfer taking place in boiler walls, fins etc are the examples of conduction heat transfer.
Newton's law of momentum diffusion states that momentum flux is proportional to the gradient of velocity. The proportionality constant of this relation is the fluid property (viscosity) which depends mainly on temperature of the fluid. Presence of boundary layer near the wall, in case of fluid flow over the same, is the example of momentum diffusion.
Transport equations have flux equated with gradient where only first derivatives appear in gradient terms. The reason behind this is that, diffusion is the microscopic phenomenon hence it does not account for curvature involved with higher derivatives. Along with this there is no higher power term in this equation since these equations are valid for small concentration gradients but it has been seen that these equations hold good for higher concentrations also.
1.4.3. Compressibility of fluid and flow:
If application of pressure changes volume or density of the fluid then fluid is said to be compressible.
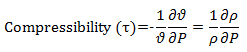
Compressibility is thus inverse of bulk modulus. Hence compressibility can be defined as the incurred volummetric strain for unit change in pressure. Negative sign in the above expression is the fact that volume decreases with increase in applied pressure. For example, air is more compressible than water. Since definition of compressibility involves change in volume due to change in pressure, hence compressibility can be isothermal, where volume change takes place at constant temperature or isentropic where volume change takes place at constant entropy.
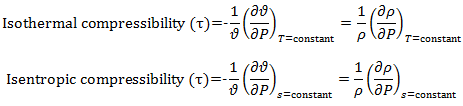
Also, for isothermal compressibility we know,
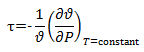
Since ![]() for ideal gas, we have,
for ideal gas, we have,
![]()
Hence, isothermal compressibility is
|
(1.7) |
For isentropic compressibility we know,
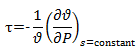
Since, Pvγ = constant for isentropic process for an ideal gas, we have,
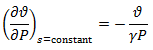
Hence, isentropic compressibility is
|
(1.8) |
Comparing equations (1.7) and (1.8) we can see that, isothermal compressibility is always higher than isentropic compressibility of gas since specific heat ratio is always greater than one. This inturn means that it is simpler to change the volume of a gas isothermally than isentropically. In otherwards, it means that we need lesser amount of pressure to bring a particular amount of change in volume during isothermal process than during isentropic process.
Fluid flow is said to be compressible if density of the fluid changes roughly 5% of its original density during its flow.
![]()
From this relation it is very clear that, percenetage change in density of fluid flow will be higher if either compressibility of the fluid is higher or pressure difference is high. Hence, compressible fluids exposed to smaller pressure difference situations can exhibit incompressible flow and at the same time incompressible fluids exposed to high pressure difference situations can exhibit compressible flow.