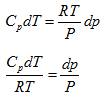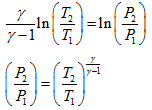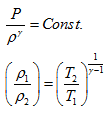For the special case, if system undergoes reversible adiabatic or isentropic process then, entropy change of the system (dS ) is zero. Therefore equation 1.3 can be written as,
CpdT = vdp
From ideal gas realation, v = RT/P, above equations becomes
|
(1.4) |
We know the relations between specific heats as
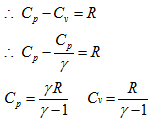
Substituing above expression for Cp in equation (1.4), we get
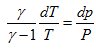
Integrating above equation from state 1 to state 2 for the isentropic process of the system, we get,
|
(1.5) |
Since the system is undergoing adiabatic process from state 1 to state 2,
|
(1.6) |
Here relations 1.5 and 1.6 are called as Isentropic equations.
1.4. Important Fluid Properties
1.4.1 Continuum:
Fluid matter is made up of molecules or atoms. However for most of the fluid dynamic calcultions discrete presene of these elementray objects is neglected and fluid matter is assumed to be continuous for prediction of various fluid flow phenonmenon or for mesurement of fluid properties. If a pressure probe concentrates to a very small area, of molecular dimensions, in the fluid flow, then fluctuations can be observed in the measurements due to random presence of molecules. Therefore any measurement probe used for experiments or fluid property estimation should not have very small probe area in order to incur molecular flactuations. If average number of molecules colliding the probing area over the time is very large then these flacutaions die out and we get a constant macroscopic value of the property. For these conditions we can comfortably make the assumptions of continuum of matter.
Continuous presence of the matter is called as continuum. This is the assumption which we will be using for most of the derivations of this course. This assumption helps us for calculation of gradient and flow variables smoothly. The governing non-dimensional parameter for prediction of continuum is Knudsen number which is defined as the ratio of mean free path to the characteristic length of the object. Here mean free path should be understood as the mean distance traveled by a molecule between two successive collisions with other molecules. Thus calculated Knudsen number should be close to zero or below 0.3 for use of most of the relations or governing equations. Mean free path of standard atmosphere is 5 x 10-8 m due to very high density of air near the earth’s surface. Therefore Knudsen number reamins close to zero for general fluid dynamic situations. Validation of continuum assumption and in turn the usage of governing equations in their standard form remain intact till the altitude of around 90 km from earth surface where Knudsen number is below 0.3.
Above the first critical value of Knudsen number (0.3) , usefulness of governig equations in their stardard form is intact however the nature of boundary conditions change due to existance of velocity and temperature slip on the wall. From 90 Km till 150 km from earth surface, density becomes low as a effect of which fluid velocity and temperature at the surface do not remain in equilibrium with the surface. Therefore for the Knudsen number range 0.3 to 1, which is also called as transitional regime, slip wall boundary conditions should be used along with the usual governing equations based on continuum assumption
Presence of free molecular flow can be assured If Knudsen number crosses 1. Kinetic theory of gases and related equations are generally prescribed if the Knudsen number crosses its second critical value. This conditions persists beyond. 150 km from earth’s surface where density of air is very low.