Problem 3
An equilateral triangular prism 20 mm side of base and 50 mm long rests with one of its shorter edges on HP such that the rectangular face containing the edge on which the prism rests is inclined at 300 to HP. The edge on which prism rests is inclined at 600 to VP. Draw its projections.
Solution: The procedure of obtaining the projections is shown in figure 8. The prism rests with one of its shorter edges, i.e., triangular or base edge on HP such that the rectangular face containing that edge is inclined at 300 to HP.
Draw the simple views of the prism when it rests with one of its triangular faces, i.e., base completely lying on HP and also with one of its shorter edges perpendicular to VP, i.e., to XY line. The shorter edge (b1)(c1) is perpendicular to the XY line. The rectangular face containing the edge b1’(c1’) is b1’b’(c’)(c1’).
Now tilt the prism on the edge b1’(c1’) such that the rectangular face b1’b’(c’)(c1’) is inclined at 300 to the XY line. In this tilted position, project the top view.
It is seen that the edge b1c1 in the top view shown is perpendicular to VP, i.e, to XY line. But the edge b1c1 has to be inclined at 600 to VP, i.e, to XY line. Therefore, reproduce the top view with the edge b1c1 inclined at 600 to the XY line as shown in the top view.
Project the reproduced top view to get the front view.
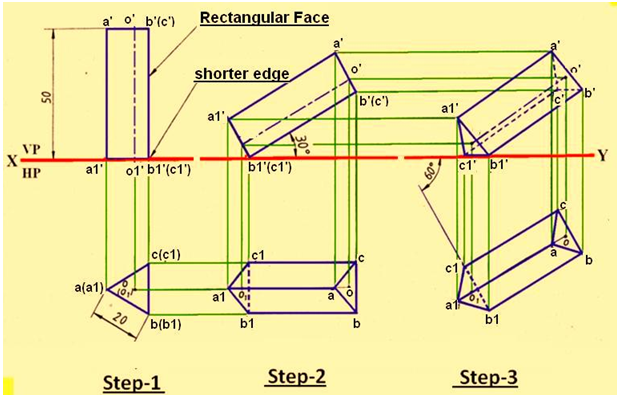
Figure 3. The projections of the triangular prism of problem-3