Problem 1.
A cube of 30 mm sides is held on one of its corners on HP such that the bottom square face containing that corner is inclined at 300 to HP. Two of its adjacent base edges containing the corner on which it rests are equally inclined to VP. Draw the top and front views of the cube.
Solution:
The procedure of obtaining the projections is shown in figure 6. InStep-1, the projections of the cube is drawn in the simple position. The cube is assumed to lie with one of its faces completely on HP such that two vertical faces make equal inclinations with VP. Draw a square abcd to represent the top view of the cube such that two of its sides make equal inclinations with the XY line, i.e., with VP. Let (a1), (b1), (c1) and (d1) be the four corners of the bottom face of the cube which coincide in the top view with the corners a, b, c and d of the top face. Project the front view of the cube. The bottom face a1’b1’c1’(d1’) in the front view coincide with the XY line. Now the cube is tilted on the bottom right corner c1’ (step-2) such that the bottom face a1’b1’c1’(d1’) is inclined at 300 to HP. Reproduce the front view with face a1’b1’c1’(d1’) inclined at 300 to the XY line.
Draw the vertical projectors through all the corners in the reproduced front view and horizontal projectors through the corners of the first top view. These projectors intersect each other to give the corresponding corners in the top view
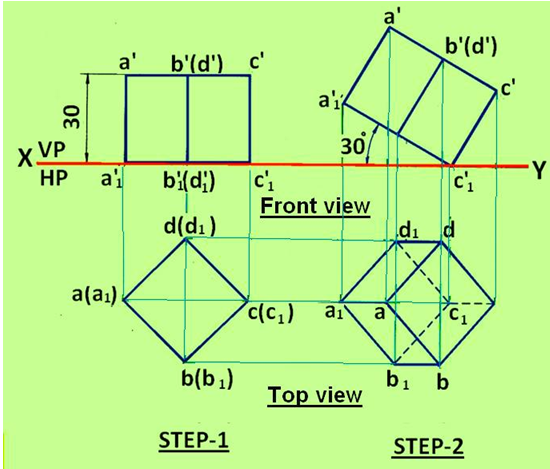
Figure 1. The projections of the cube of problem 1.