Constructing a Parabola (Parallelogram Method)

Parabola can also be constructed by parallelogram method. This is illustrated by the example below and shown in figure 4.
Example: Draw a parabola of base 100 mm and axis 50 mm if the axis makes 70° to the base.

1. Draw the base RS = 100 mm and through its midpoint K, draw the axis KV = 50 mm, inclined at 70° to RS. Draw a parallelogram RSMN such that SM is parallel and equal to KV.
2. Divide RN and RK into the same number of equal parts, say 5. Number the divisions as 1, 2, 3, 4 and 1’, 2’, 3’, 4’, starting from R.
3. Join V–1, V–2, V–3 and V–4. Through 1’, 2’, 3’ and 4’, draw lines parallel to KV to meet V–1 at P1, V–2 at P2, V–3 at P3 and V–4 at P4, respectively.
4. Obtain P5, P6, P7 and P8 in the other half of the rectangle in a similar way. Alternatively, these points can be obtained by drawing lines parallel to RS through P1, P2, P3 and P4. For example, draw P1– P8 such that P1– x = x– P8. Join P1, P2, P3 … P8 to obtain the parabola.

 

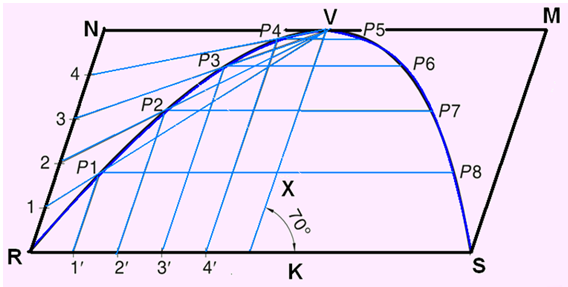
Figure 4. Construction of parabola by parallelogram method.

Tangent Method

This method can be used  when the base and the axis, or base and the inclinations of tangents at open ends of the parabola with the base are given. The method is shown in figure 5.

This method can be used  when the base and the axis, or base and the inclinations of tangents at open ends of the parabola with the base are given. The method is shown in figure 5.
Draw the line AB representing the base of the parabola.
Draw the Axis EF representing the height of the parabola.
Produce EF to O such that EF = OF
Join OA and OB
Divide OA and OB in to  the same number of parts say 8
Mark the division points as shown
Draw lines joining 1 to 1’, 2 to 2’, 3 to 3’, etc.
Draw a curve starting from A  and tangent to the  lines 1-1’, 2-2’, 3-3’, etc, which is the required parabola.

 

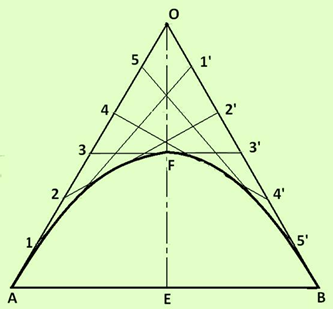
Figure 5. Tangent method of drawing a parabola.