Constructing a Parabola (Eccentricity Method)

The method of constructing a parabola by the eccentricity  method where the distance of the focus from the directrix is 60 mm  is shown in figure 3 and explained below.

1. Draw directrix AB and axis CC’ as shown.
2. Mark F on CC’ such that CF = 60 mm.
3. Mark V at the midpoint of CF. Therefore, e = VF/ VC = 1.
4. At V, erect a perpendicular VB = VF. Join CB.
5. Mark a few points, say, 1, 2, 3, … on VC’ and erect perpendiculars through them meeting CB produced at 1’, 2’, 3’, …
6. With F as a centre and radius = 1–1’, cut two arcs on the perpendicular through 1 to locate P1 and P1’. Similarly, with F as a centre and radii = 2–2’, 3–3’, etc., cut arcs on the corresponding perpendiculars to locate P2 and P2’, P3 and P3’, etc.
7. Draw a smooth curve passing through V, P1, P2, P3 … P3’, P2’, P1’.

 

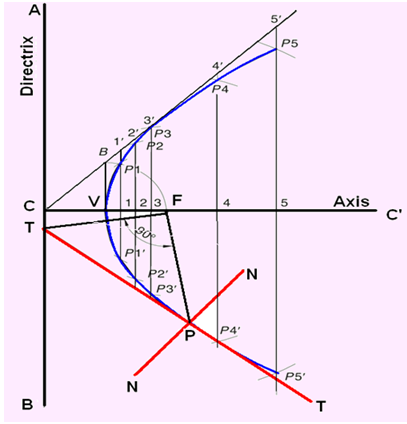
Figure 3. Construction of parabola by eccentricity method.