Epicycloid
Epicycloid is the curve generated by a point on the circumference of a circle which rolls without slipping along another circle outside it. This is illustrated in figure 2.

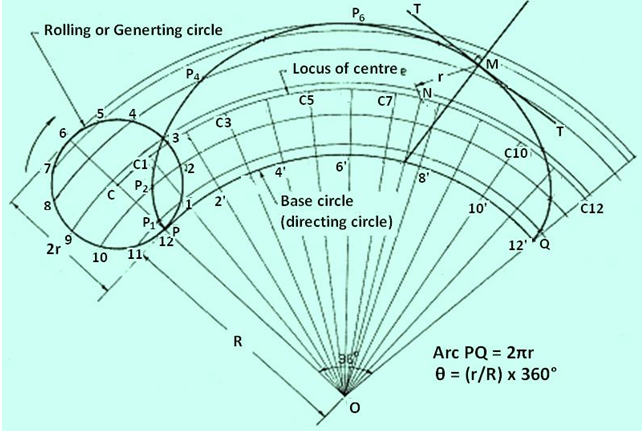
Figure 2. Illustrates  the generation of an epicycloid.

With O as centre and radius OP (base circle radius), draw an arc PQ. The included angle θ = (r/R) x 360°. With O as centre and OC as radius, draw an arc to represent locus of centre.
Divide arc PQ in to 12 equal parts and name them as 1’, 2’, …., 12’. Join O1’, O2’, … and produce them to cut the locus of centres at C1, C2, ….C12. Taking C1 as centre, and radius equal to r, draw an arc cutting the arc through 1 at P1. Taking C2 as centre and with the same radius, draw an arc cutting the arc through 2 at P2Similarly obtain points  P3, P3, …., P12. Draw a smooth curve passing through P1, P2….. , P12, which is the required epiclycloid.

Hypocycloid
 Hypocycloid is the curve generated by a point on the circumference of a circle which rolls without slipping inside another circle.

The construction of a hypocycloid is illustrated in figure 3.

 

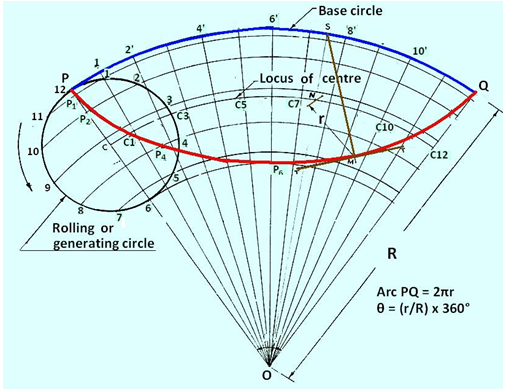
Figure 3  Construction of a hypocycloid.

With O as centre and radius OP (base circle radius), draw an arc PQ. The included angle θ = (r/R) x 360°. With O as centre and OC as radius, draw an arc to represent locus of centre.
Divide arc PQ in to 12 equal parts and name them as 1’, 2’, …., 12’. Join O1’, O2’, …, O12’  so as to cut the locus of centres at C1, C2, ….C12. Taking C1 as centre, and radius equal to r, draw an arc cutting the arc through 1 at P1. Taking C2 as centre and with the same radius, draw an arc cutting the arc through 2 at P2. Similarly obtain points  P3, P3, …., P12. Draw a smooth curve passing through P1, P2….. , P12, which is the required hypocycloid.