Table 1 Classification of Cycloidal curve

	Generating Circle
		On the directing line	Outside the directing line	Inside the directing line
Generating  point	On the generating circle	Cycloid	Epicycloid	Hypocycloid
	Outside the generating circle	Superior trochoid	Superior epitrochoid	Superior Hypotrochoid
	Inside the generating circle	Inferior trochoid	Inferior epitrochoid	Inferior hypotrochoid

Cycloid
A Cycloid is generated by a point on the circumference of a circle rolling along a straight line without slipping.
The rolling circle is called the Generating circle
The straight line is called the Directing line or Base line

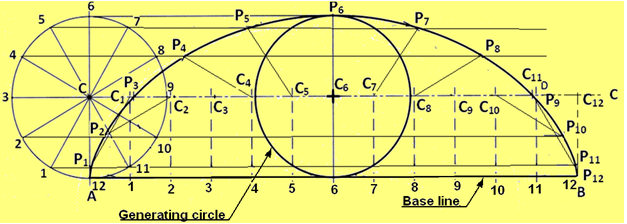
Figure 1 illustrates the procedure for drawing a cycloid.

Generating circle has its center at C and has a radius of C-P’. Straight line PP’ is equal in length to the circumference of the circle and is tangent to the circle at point P’. Divide the circle into a number of equal segments, such as 12.  Number the intersections of the radii and the circle.  From each point of intersection on the circle, draw a construction line parallel to line PP’ and  extending up to line P’C’.  Divide the line CC’ into the same number of equal parts, and number them. Draw vertical lines from each point to intersect the extended horizontal centerline of the circle.  Label each point as C1, C2, C3, …. C12.
Using point C1 as the center and radius of the circle C-P’, draw an arc that intersects the horizontal line extended from point 1 at P1.  Set the compass at point C2, then draw an arc that intersects the horizontal line passing through point 2 at P2.  Repeat this process using points C3, C4, …. C12, to locate points along the horizontal line  extended from points 3, 4, 5, etc.. Draw a smooth curve connecting  P1, P2, P3, etc to form the cycloid