Normal and tangent to an Archemedian spiral.
The normal to an Archemedian Spiral at any point is the hypotenuse of the right angles triangle having the
other two sides equal to the length of the radius vector at that point and the constant of the curve
The constant of the curve is equal to the difference between the length of  any two radii divided by the
circular measure of the angle between them.
The steps followed to draw the normal and tangent to a spiral at any point N is illustrated in figure 5.
Draw the radius vector ON
Draw OM perpendicular to ON and length equal to the constant of the curve.
Join MN
MN is the normal at point N
Draw PQ perpendicular to MN to obtain  the tangent at N.

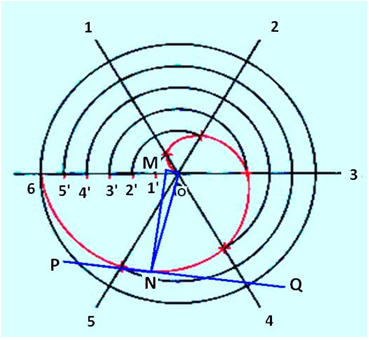
Figure 5. Drawing a tangent and normal to the spiral at any point.