Logarithmic spiral
In logarithmic spiral, the ratio of the lengths of consecutive radius vectors enclosing equal angles always remains constant. i.e. the values of vectorial angles are in arithmetical progression .  The  corresponding values of radius vectors arte in geometric progression.
The construction of a logarithmic spiral is illustrated in figure 4  as solution to the following problem.
Problem: Ratio of lengths of radius vectors enclosing angle of 30° = 6:5. Final radius vector of the spiral is  90 mm. Draw the spiral.
Solution:
Draw line AB and AC inclined at 30°. 
On line AB, mark A-12 = 90 mm.
A as center and A12 radius draw an arc to cut AC at 12΄.
Mark A11 (= 5/6 of A12) on AB. Join 12΄ and 11.
Draw an arc with A as center and A11 radius to cut the line AC at 11΄.
Draw a line through 11΄  parallel to 12΄-11 to cut AB at 10.
Repeat the procedure to obtain points 9΄, 8΄, 7΄…0.
OP12 = A12΄, OP11 = A11΄….

 

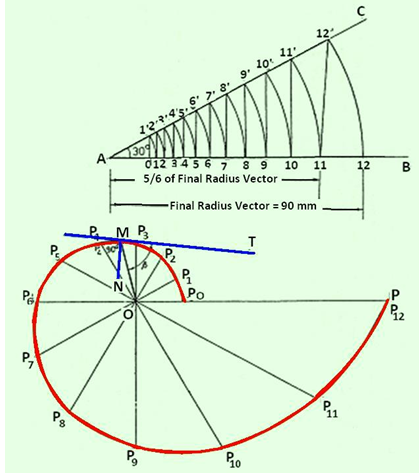
Figure 4. Logarithmic spiral