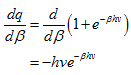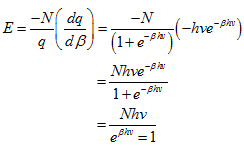Example 1: Calculate the number of ways of arranging seven distinguishable particles in four boxes so that Ni = 1, N2 = 2, N3 = 3 and N4 = 4
Solution:
We know that
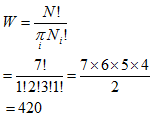
Example 2: Calculate the number of ways of arranging six indistinguishable particles in four boxes which are (a) distinguishable, (b) indistinguishable
Solution:
Since the boxes are distinguishable,
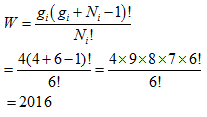
If the boxes are indistinguishable, then
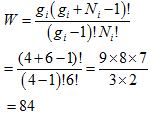
Example 3: Consider a cubical box of edge 20 cm, containing gaseous helium at 400 K. Evaluate the energy εx and its corresponding nx.
Solution: We know that
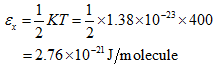
For x - directional component,
![]()
where a is the side of the cubical box.
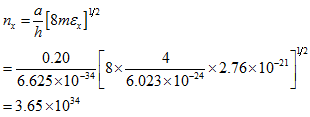
Example 4: (a) Consider the motion of 2 kg mass at a velocity of 2 m/s. Estimate the characteristic wavelength for this motion.
(b) Consider the motion of an electron having a mass of 9.106 X 10-31 kg at a velocity of 108 m/s. Calculate the characteristic wavelength in this case.
Solution:
(a)The de Broglie wavelength is:
![]()
(b) Neglecting relativistic effects, the wavelength is:
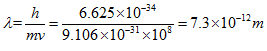
Example 5: (a) Consider a system of N particles and a phase space of two cells, and take g1 = g2 = 1. If the energy ε of a particle is the same in both the cells, find the number of particles in each cell and the total energy of the system in equilibrium.
(b) If ε1 = 0 and ε2 = ε, find the number of particles in each cell and the total energy of the same system in equilibrium.
(c) Find the values of the total energy for the case (b) when T = 0 and when T = ∞
Solution:
The partition function
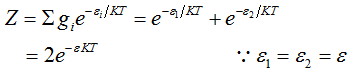
At equilibrium we know that
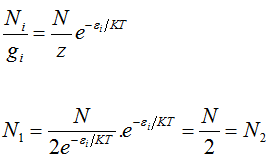
The particles are, therefore, uniformly distributed in the two cells.
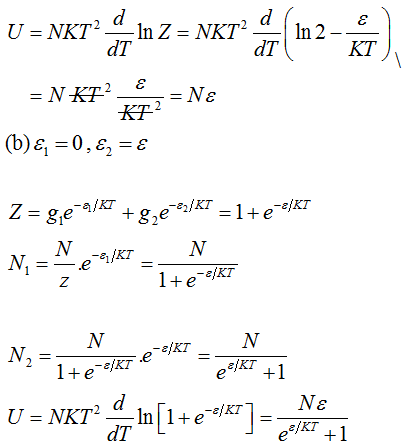
(c)When T = 0 K, U = 0
T = ∞, U = Nε/2
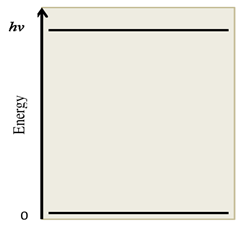
Example 6: Determine the total energy of an ensemble consisting of N particles that have only two energy levels separated by hν.
Solution:
The energy levels for the particles are illustrated in Fig A. As mentioned, systems with only two energy levels are commonly referred to as two-level systems. To determine the average energy, the partition function describing this system must be evaluated. The partition function consists of a sum of two terms as follows:
q = 1 + e-βhν
The derivative of the partition function with respect to β is
Using this result, the total energy is
|
Fig. A Energy Levels for a particle |