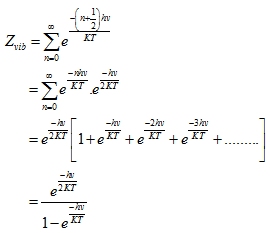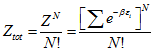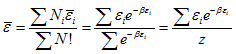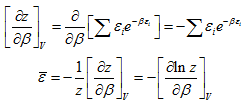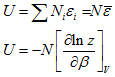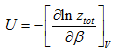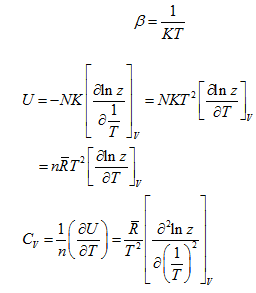Thermodynamic Properties
A partition function is the essential link between the coordinates of microscopic systems and the thermodynamic properties. Once it has been evaluated, all the physical properties, such as U, S, c_p, c_v etc. can be estimated.
Energy may be stored in a molecule in various modes. The total energy of a molecule is

(5.216)

The degeneracies of an energy level are multiplicative:

(5.217)

The partition function is the summation over all energy levels accessible to the molecule:

(5.218)

Therefore, partition function Z is also multiplicative.

(5.219)

To determine the partition function of a molecule, it is necessary to find each of the contributing partition functions.

(5.220)

The energy levels of a simple harmonic oscillator are

(5.221)

With g_i = 1,

(5.222)

Similarly, Z_rot, Z_chem,......etc. are to be evaluated.
So far z refers to a single particle. The total partition function of N identical distinguishable particles:

(5.223)

For N indistinguishable particles,

(5.224)

Internal Energy

Average energy of particle is'

(5.225)

Now,

(5.226)

The internal energy of system is

(5.227)

In terms of Z_tot,

(5.228)

Now

(5.229)     (5.230)