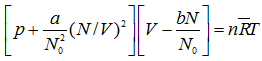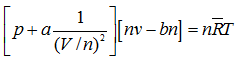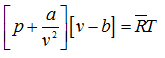van der waals Equation of state
van der Waals introduced in the ideal gas equation of state a second correction term to take into account the intermolecular forces. The forces of attraction among molecules decrease rapidly with distance (e.g., as 1 / r6 ). Although the molecules within the gas are, on the average, attracted equally in all directions, those in the outermost layer experience a net inward force, as a result of which the pressure measured is less.
If p' represents the pressure computed from consideration of molecular impacts, the reduction of the observed pressure from consideration of molecular impacts, the reduction of the observed pressure below p' is proportional to (N / V)2 or equal to a'(N / V)2, where a' is a constant. The observed pressure p can, therefore, be written as
|
(4.60) |
or,
|
(4.61) |
From Eqs (4.59) and (4.61),
|
(4.62) |
Let 
and 
where N0 is the Avogadro’s number, then the above equation reduces to
|
(4.63) |
or,
|
(4.64) |
or,
|
(4.65) |
where v is the molar volume (m3/kgmol). This is known as the van der Waals equation of state.