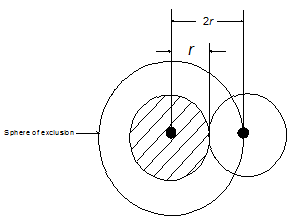
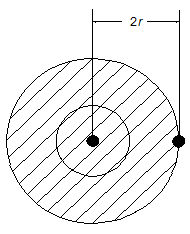
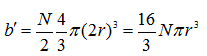Let us imagine that a certain instant all the molecules of a gas in certain volume V, except one,  are “frozen” in their respective sites, while the remaining molecule continues to move and collide with others. The molecules are rigid spheres of radius r.  At the instant of collision, the centre-to-centre distance between the two molecules is 2r (Fig. 4.11), which would remain the same if the moving molecule is shrunk to a geometric point while the other is increased to radius 2r. It is seen that the locus of the center of one molecule revolving about the other is a sphere of radius 2r This is called the “sphere of exclusion”, which means that the center of the moving molecule never gets closer than 2r to the center of the other molecule .Thus , the exclusive volume of one molecule that cannot be entered by another molecule is

Fig. 4.11 (a) Actual Collision	Fig. 4.12 (b) Sphere of exclusion

(4.56)

since one-half of the total number of molecules excludes the other half (two molecules are required to cause a collision). Volume of one molecule is  the unavailable volume b' is

total molecule volume

(4.57)

Therefore, the available volume is (V - b'). From Eq.(6.27),

(4.58)

and replacing  by we get

(4.59)

This is known as the Clausius equation of state.