We can use Newton 's equations for particles to derive the equations of motion of a rigid body. A rigid body, which is constrained to move in a plane, has three degrees of freedom, and hence it has three independent equations of motion which relate the forces in the plane to accelerations. Consider the body shown in Fig. 1.1 (a). A set of forces 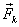 and couples and couples 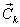 act on it, with the force act on it, with the force 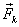 acting at the point acting at the point 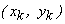 . The position coordinates are with respect to an inertial frame. The rigid body can be considered to be made of elemental masses which can be regarded as particles. Newton 's equation for the . The position coordinates are with respect to an inertial frame. The rigid body can be considered to be made of elemental masses which can be regarded as particles. Newton 's equation for the 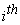 elemental mass elemental mass 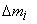 (Fig. 1.1 (b)) at the location (Fig. 1.1 (b)) at the location 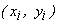 is is |