| |
Regions of absolute stability for these methods may be found is Gear; for 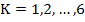 , all regions are finite, and the corresponding methods are stiffly stable and , all regions are finite, and the corresponding methods are stiffly stable and 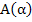 –stable. –stable.
Finally, if we settle for something less than 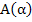 -stability, the methods proposed by Robertson are of interest. These comprise a one-parameter family obtained by taking the following linear combination of Simpson's rule and the two-step Adams-Moultan method: -stability, the methods proposed by Robertson are of interest. These comprise a one-parameter family obtained by taking the following linear combination of Simpson's rule and the two-step Adams-Moultan method:
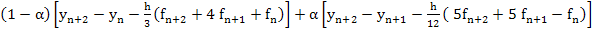 , 0 , 0 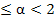
These methods have order three if 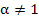 and the regions of absolute stability are large, almost circular, regions in the half plane and the regions of absolute stability are large, almost circular, regions in the half plane 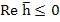 , the intervals of absolute stability being , the intervals of absolute stability being 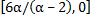 . (Note that as . (Note that as 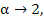 zero instability threatens). Such methods are appropriate for moderately stiff systems. zero instability threatens). Such methods are appropriate for moderately stiff systems. |