Runge-Kutta methods for Stiff systems

Explicit Runge-Kutta methods have rather small regions of absolute stability. On the other hand it is rather easier to find A-stable implicit Runge-Kutta methods than to find A-stable implicit linear multistep methods. For example, Ehle has shown that Butcher's R-stage implicit Runge-Kutta methods of order 2 R, namely

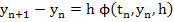
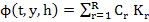
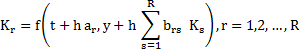
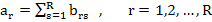
[The functions 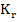are no longer defined explicitly but by a set of R implicit equations, in general non linear.]

are all A-stable; thus there exist A-stable methods of this type of arbitrarily high order. L-stable implicit Runge-Kutta methods are also possible.

However, all such methods suffer a serious practical disadvantage in that the solution of the implicit nonlinear equations at each step is considerably harder to achieve in the case of implicit Runge-Kutta methods than in the case of implicit linear multistep methods. If we consider the R-stage fully implicit Runge-Kutta method given above, applied to a m-dimensional stiff system, then it is clear that the 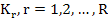are also m-vectors. It follows that at each step we have to solve a system of m R simultaneous nonlinear equations by some form of Newton-iteration and this will converge only if we can find a suitably accurate initial iterate. This constitutes a formidable computational task.

If the Runge-Kutta method is semi-explicit, then the m R simultaneous equations split into R distinct sets of equations, each set containing m equations- a less daunting prospect. The class of semi- explicit methods developed by Butcher, namely [ That an R-stage semi explicit method can attain higher order than an R-stage explicit method is demonstrated by the following fourth-order three-stage method quoted by Butcher]

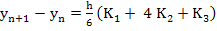
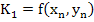
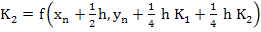
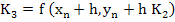
are not, however, A-stable.

It is clear from the above discussion that our troubles with stiff systems are not over when we find as A-or L-stable method; the real test is the efficiency with which we can handle the resultant implicitness.