| |
Backward Differentiation Methods
Let us now consider linear multistep methods which are not necessarily A-stable, but are 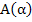 -stable or stiffly stable. Since stiff stability implies -stable or stiffly stable. Since stiff stability implies 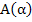 -stability for some -stability for some 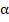 , we need, in view of the theorem, look only at implicit linear multistep methods. With the usual notation for the characteristic polynomials of a linear multistep method, the associated stability polynomial is , we need, in view of the theorem, look only at implicit linear multistep methods. With the usual notation for the characteristic polynomials of a linear multistep method, the associated stability polynomial is 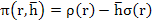 . Both . Both 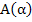 and stiff stability require that the roots of and stiff stability require that the roots of 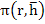 be inside the unit circle when be inside the unit circle when 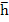 is real and is real and 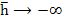 . In this limit, the roots of . In this limit, the roots of 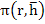 approach those of approach those of 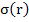 , and it is thus natural to choose , and it is thus natural to choose 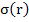 so that its roots lie within the unit circle. In particular, the choice so that its roots lie within the unit circle. In particular, the choice 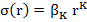 , which has all its roots at the origin, is appropriate. The resulting class of methods , which has all its roots at the origin, is appropriate. The resulting class of methods
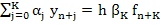 |
(9.7) |
are known as the of backward differentiation methods . The coefficients of 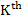 order K-step method, of this class are given in the following table for order K-step method, of this class are given in the following table for 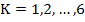 . .

|