Exponential Fitting
Definition: A numerical method is said to be exponentially fitted at a (complex) value 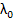 if, when the method is applied to the scalar test problem if, when the method is applied to the scalar test problem 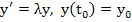 , with exact initial conditions, it yields the exact theoretical solution in the case when , with exact initial conditions, it yields the exact theoretical solution in the case when 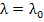 . .
The method (9.6) applied to the above test equation yields
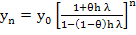
This coincides with the theoretical solution in the case 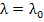 if we choose if we choose  such that such that 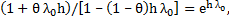
or
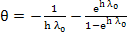 . .
Note that we can only exponentially fit the method (9.6) to one value of 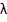 , whereas for a general stiff system, the Jacobian will have , whereas for a general stiff system, the Jacobian will have 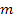 eigenvalues. Strategies for choosing the value at which (9.6) should be exponentially fitted; when we have some a-priori knowledge of the distribution of the eigen values of the Jacobian are discussed by Liniger and Willoughby. If we have no such knowledge, Liniger proposes eigenvalues. Strategies for choosing the value at which (9.6) should be exponentially fitted; when we have some a-priori knowledge of the distribution of the eigen values of the Jacobian are discussed by Liniger and Willoughby. If we have no such knowledge, Liniger proposes  be chosen to minimize be chosen to minimize
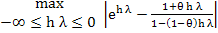
The value of  which achieves this minimization is which achieves this minimization is 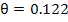 . .
There is no point is looking for A-stable methods in the one-parameter family of implicit linear two-step methods since they all have order at least three, and so cannot be A-stable. However, if we retain a second parameter, we may write the family in the form
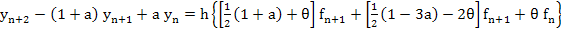 |
(9.7) |
which now has order two in general. It is shown by liniger that methods of this family are A-stable if and only if 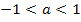 and and 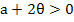 . (Note that the first of these conditions implies zero stability). . (Note that the first of these conditions implies zero stability). |