A-stable linear multistep methods must be implicit, and have order not greater than two. The best known A-stable method is the Trapezoidal rule, which has the additional advantage of processing an asymptotic expansion in even powers of the step length i.e.
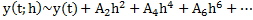
thus permitting efficient use of the extrapolation processes. Its disadvantage is that if a moderate step length is used in the initial phase, then fast decaying components of the theoretical solution are represented numerically by slowly decaying components, resulting in a slowly decaying oscillatory error. This difficultly can be avoided either by choosing a very small step length in the initial phase or by using a moderate step length and applying in the first few steps the same smooth procedure as is used in Gragg's method, that is, 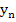 is replaced by is replaced by 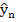 here here 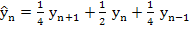 . .
This procedure preserves the form of the asymptotic expansion.
The class of linear one-step methods of order one is given by
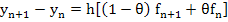 |
(9.6) |
often referred to as the ' – method'. It follows that this is A-stable if and only if – method'. It follows that this is A-stable if and only if 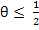 . One way in which the free parameter . One way in which the free parameter  may be used to effect is to achieve exponential fitting; a concept proposed by Liniger and Willoughby. may be used to effect is to achieve exponential fitting; a concept proposed by Liniger and Willoughby. |