The restriction on order implied by (i) is a severe one. In view of this, several less demanding stability definitions have been proposed; we present two here:
Definition: (Widlund) A numerical method is said to be 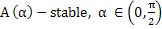 , if its region of absolute stability contains the infinite wedge , if its region of absolute stability contains the infinite wedge 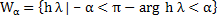 . It is said to be A(0)-stable if it is . It is said to be A(0)-stable if it is 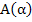 -stable for some(sufficiently small) -stable for some(sufficiently small) 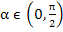
Theorem: (i) An explicit linear multistep method cannot be A(0)-stable. (ii) There is only one A(0)-stable linear K-step method whose order exceeds 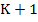 , namely the trapezoidal rule, (iii) For all , namely the trapezoidal rule, (iii) For all 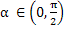 , there exist , there exist 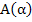 -stable linear K-step methods of order -stable linear K-step methods of order 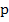 for which for which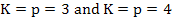 . .
An alternative slackening of the A-stability requirement is incorporated in the following definitions:
Definition (Gear): A numerical method is said to be stiffly stable if (i) its region of absolute stability contains 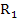 and and 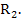 and (ii) it is accurate for all and (ii) it is accurate for all 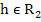 when applied to the scalar test equation when applied to the scalar test equation 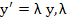 a complex constant with a complex constant with 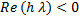 , where , where
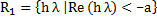 , ,
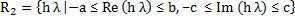
and a, b, and c are positive constants.
The motivation for this definition is that those eigen values which represent rapidly decaying terms in the transient solution will correspond to values of 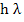 in in 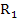 ; we generally have no interest in representing such terms accurately but only stably-that is, we will be satisfied with any representation of these terms which decays sufficiently rapidly. The remaining eigen values of the system represent terms in the solution which we would like to represent accurately as well as stably; by suitable choice of ; we generally have no interest in representing such terms accurately but only stably-that is, we will be satisfied with any representation of these terms which decays sufficiently rapidly. The remaining eigen values of the system represent terms in the solution which we would like to represent accurately as well as stably; by suitable choice of 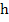 , values of , values of 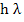 corresponding corresponding 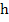 these eigen values can be made to lie in these eigen values can be made to lie in 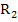 . . |