A-Stability Versus L-Stability
Severe as the requirement of A-stability is, in one sense it is not severe enough. Consider, for example, the application of the Trapezoidal rule to the scalar test equation 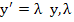 a complex constant with a complex constant with 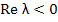 . We obtain . We obtain
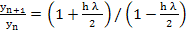
Since the Trapezoidal rule is A-stable, 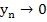 , as , as 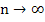 for all fixed for all fixed 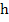 . .
However,
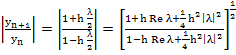
and if 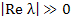 and and 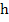 is not small then is not small then 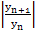 will be close to will be close to 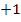 . Thus . Thus 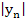 will decay to zero only very slowly, and it follows that an A-stable method may be unsatisfactory for an excessively stiff system. Contrast the behavior of the method will decay to zero only very slowly, and it follows that an A-stable method may be unsatisfactory for an excessively stiff system. Contrast the behavior of the method 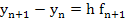 [the backward Euler method) for which [the backward Euler method) for which
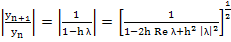
and the RHS tends to zero as 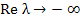 and we can expect a rapid decay of and we can expect a rapid decay of 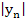 even for moderately large even for moderately large 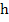 . .
Definition: (Ehle) A one step method is said to be L-stable if it is A-stable and, in addition, when applied to the scalar test equation 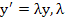 a complex constant with a complex constant with 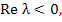 it yields it yields 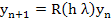 , where , where 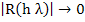 as as 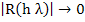 . Note that . Note that 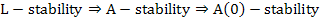 |