The problem of stability for stiff systems
We have seen that a basic difficulty (but not the only one) in the numerical solution of stiff systems is the satisfaction of the requirement of absolute stability. Thus, several definitions which call for the method to possess some adequate region of absolute stability, have been proposed.
Definition: (Dahlquist) A numerical method is said to be A-stable if its region of absolute stability contains the whole of the left-hand half-plane 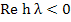 . .
If an A-stable method is applied to a stiff system, then the difficulties described earlier disappear, since, no matter, how large 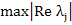 , no stability restriction on , no stability restriction on 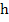 can result. However, A-stability is a severe requirement to ask of a numerical method as the following somewhat depressing theorem of Dahlquist shows: can result. However, A-stability is a severe requirement to ask of a numerical method as the following somewhat depressing theorem of Dahlquist shows:
Theorem: (i) An explicit linear multistep method cannot be A-stable. (ii) The order of an A-stable implicit linear multistep method cannot exceed two. (iii) The second order A-stable implicit linear multistep method with smallest error constant is the Trapezoidal rule. |