| |
Definition: The linear systems 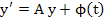 is said to be stiff if (i) is said to be stiff if (i) 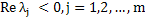 and (ii) and (ii) 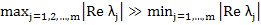 , where , where 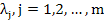 are the eigen values of A. The ratio are the eigen values of A. The ratio
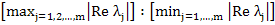
is called the stiffness ratio.
Non linear systems 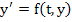 exhibit stiffness if the eigen values of the Jacobian exhibit stiffness if the eigen values of the Jacobian 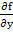 behave in a similar fashion. The eigen values are no longer constant but depend on the solution, and therefore vary with behave in a similar fashion. The eigen values are no longer constant but depend on the solution, and therefore vary with 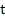 . Accordingly we say that the system . Accordingly we say that the system 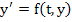 is stiff in an interval is stiff in an interval 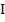 of of 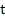 if, for if, for 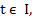 the eigen values the eigen values 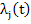 of of 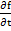 satisfy (i) and (ii) above. satisfy (i) and (ii) above.
Note that if the partial derivatives appearing in the Jacobian 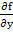 are continuous and bounded in an appropriate region, then the Lipschitz constant are continuous and bounded in an appropriate region, then the Lipschitz constant 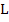 of the system of the system 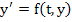 may be taken to be may be taken to be 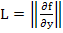 . For any matrix . For any matrix 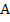 , , 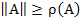 where where 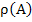 is the spectral radius, is defined to be is the spectral radius, is defined to be 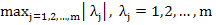 being the eigen values of being the eigen values of 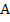 . If . If 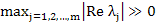 it follows that it follows that 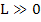 . Thus stiff systems are occasionally referred to as systems with large Lipschitz constants'. . Thus stiff systems are occasionally referred to as systems with large Lipschitz constants'.
|