Theorem 2: A necessary condition for convergence of the linear multistep method defined by (8.11) is that the order of the associated difference operator be at least 1.
The condition that the order 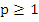 is called the condition of consistency. In terms of the constants introduced earlier (in associated difference operator) the condition is equivalent to is called the condition of consistency. In terms of the constants introduced earlier (in associated difference operator) the condition is equivalent to 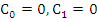 ; in terms of the polynomials ; in terms of the polynomials 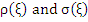 , the condition of consistency is expressed by the relations , the condition of consistency is expressed by the relations
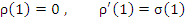 |
(8.16) |
Proof: We begin by showing that 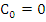 . If the method is convergent, it is convergent in the initial value problem . If the method is convergent, it is convergent in the initial value problem 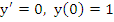 , with the exact solution , with the exact solution 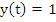 . The difference equation (8.1) again reduces to . The difference equation (8.1) again reduces to
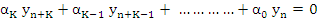 |
(8.17) |
Assuming that the method is convergent, the solution 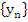 of (8.17) assuming the exact starting values of (8.17) assuming the exact starting values 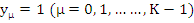 must satisfy must satisfy 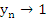 as as 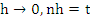 . Since in this case . Since in this case 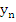 does not depend on does not depend on 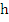 , this is the same as saying that , this is the same as saying that 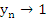 as as 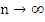 . Letting . Letting 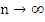 in (8.17), we obtain in (8.17), we obtain 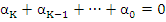 . This is equivalent to . This is equivalent to 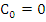 . It follows that . It follows that 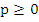 . .
|