In order to show that 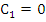 , consider the initial value problem , consider the initial value problem 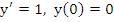 . The exact solution is . The exact solution is 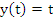 . The difference equation (8.1) now reads . The difference equation (8.1) now reads
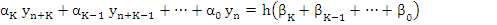 |
(8.18) |
For a convergent method every solution of (8.18) satisfying
 |
(8.19) |
where 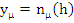 , must also satisfy , must also satisfy
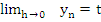 |
(8.20) |
For a convergent method we may further more assume that
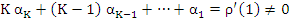
in view of the previous theorem. Let the sequence 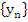 be defined by be defined by 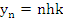 , where , where
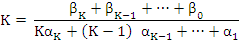
This sequence obviously satisfies (8.19) and is easily shown to be a solution of (8.18).
From
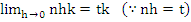 , ,
we conclude that 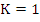 . This is equivalent to . This is equivalent to 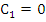 . This completes the proof of the theorem. . This completes the proof of the theorem.
|