| |
define a solution of (8.11), and they also satisfy (8.13). If the method is convergent, (8.12) must hold. If 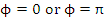 , this immediately implies , this immediately implies 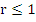 . If . If 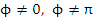 , we note that , we note that
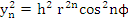
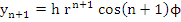
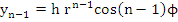
and
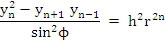
Since the term on the left tends to zero as 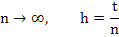 , the term on the right must do the same, which again implies , the term on the right must do the same, which again implies 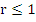 . This proves the first part of the assertion of the theorem. In order to prove the second part, assume that . This proves the first part of the assertion of the theorem. In order to prove the second part, assume that 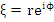 is a root of is a root of 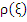 of multiplicity exceeding 1. Then, again the numbers of multiplicity exceeding 1. Then, again the numbers
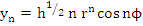 |
(8.15) |
represent a solution of (8.11). They also satisfy (8.13). Hence they must satisfy (8.12) for a convergent method. If 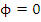 or or 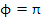 , we have for , we have for 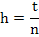 that that 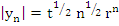 , and it follows immediately that , and it follows immediately that 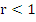 . If . If 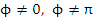 , we can make use of the relation , we can make use of the relation
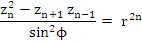
where 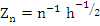 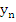 . Since . Since 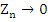 as as 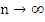 in view of (8.12), the term on the left tends to zero as in view of (8.12), the term on the left tends to zero as 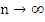 , and we conclude that , and we conclude that 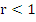 . This proves the theorem. . This proves the theorem. |